Introduction

The K-Nearest Neighbors (KNN) model is an example of a nonparametric model that can be used for classification and regression tasks. It is nonparametric in the sense that it is not defined by a fixed set of parameters, but rather retains some or all of the training examples to use in its predictions. This differs from parametric models, such as linear regression, where attempt to find the optimal parameters for some fixed mathematical function. In this post, we will explore how to implement a KNN classifier to classify iris species based on their sepal and petal measurements using the classic Iris dataset. The Iris dataset consists of 150 samples from three species of iris flowers (Iris setosa, Iris versicolor, and Iris virginica), with four features: sepal length, sepal width, petal length, and petal width.

K-Nearest Neighbors

In KNN classification, the model makes predictions based on the 'k' nearest training examples in the feature space. Given a new data point, the algorithm calculates the distance between this point and all other points in the training set, typically using Euclidean distance. It then identifies the 'k' closest points and assigns the most common class among these neighbors to the new data point. For example, in the Iris dataset, each example in the training set contains 4 features (sepal length, sepal width, petal length, petal width) and a label (the species of iris). To classify a new iris flower, we would calculate the distances to all training examples, find the 'k' nearest neighbors, and assign the species based on the majority class among those neighbors. The choice of k is important and is chosen to be an odd number so a majority class can always be determined. A small k can lead to overfitting, while a large k can smooth out the decision boundary too much.

Formally, given a training set of labeled examples $X$ and a new input point $x$, the KNN algorithm computes the predicted label $y$ by first computing: $$ d_i = \| x - x_i \|_2 $$ for each training example $x_i$ in $X$, where $\| \cdot \|_2$ denotes the Euclidean distance. This results in a sorted list of distances $$ D = \{d_1, d_2, \ldots, d_n\} \text{ such that } d_i \le d_{i+1} \text{ for all } 1 \le i < n $$ It then selects the first 'k' training examples corresponding the the sorted $d_i$ with the smallest distances and assigns the label $y$ based on the majority class among these neighbors.

Iris Classification

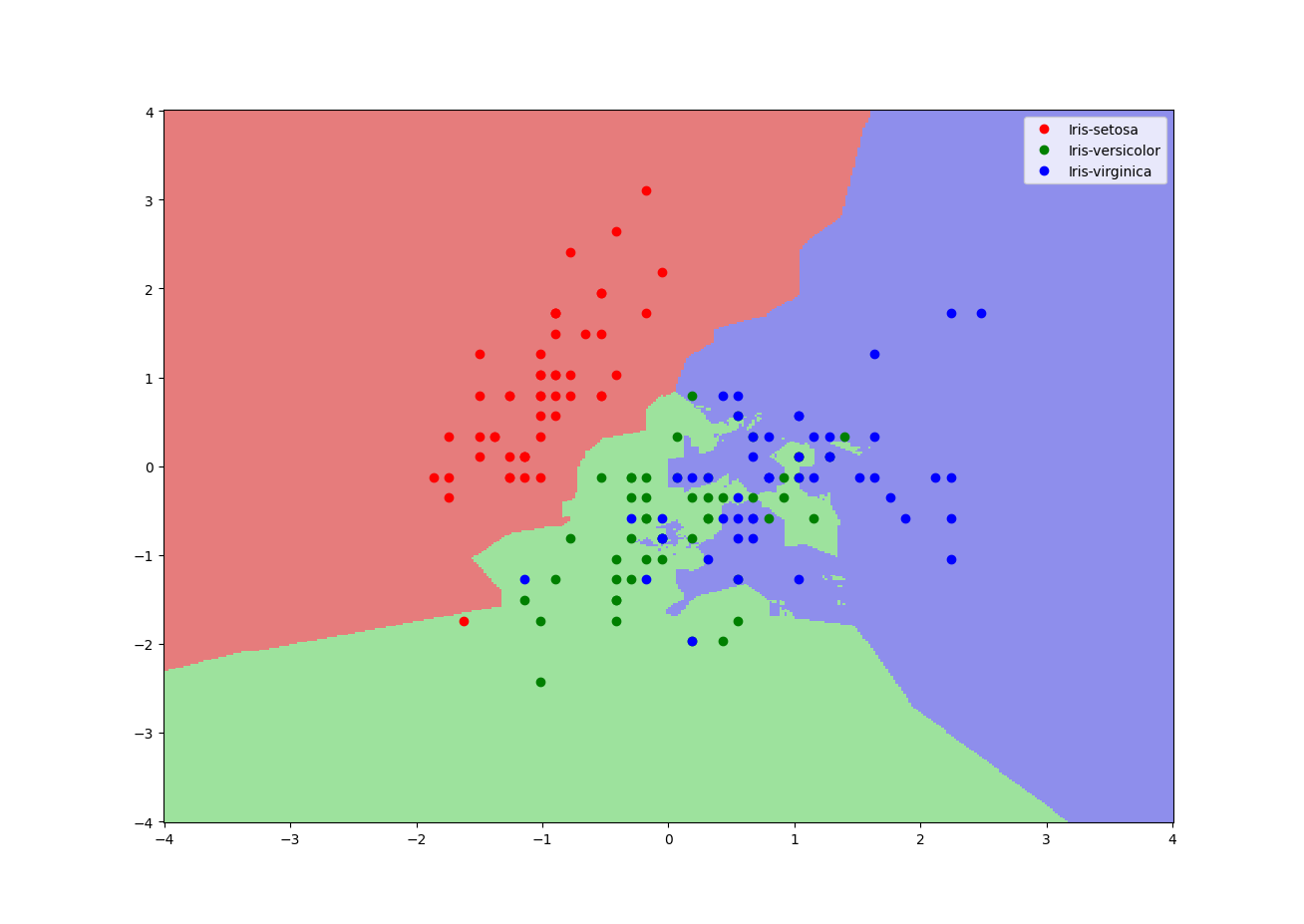
Applying the KNN algorithm to the Iris dataset, we first split the data into training and testing sets. We then standardize the feature values to ensure that all features contribute equally to the distance calculations. We choose a value for 'k' (e.g., k=3) and implement the KNN algorithm as described above. After training the model using the training set, we evaluate its performance on the test set by calculating the accuracy, which is the proportion of correctly classified instances. The KNN classifier achieves high accuracy on the Iris dataset, an accuracy of over 95%, demonstrating its effectiveness for this type of classification task. Below shows the decision boundary formed by the model in feature space using only petal length and petal width for visualization purposes.

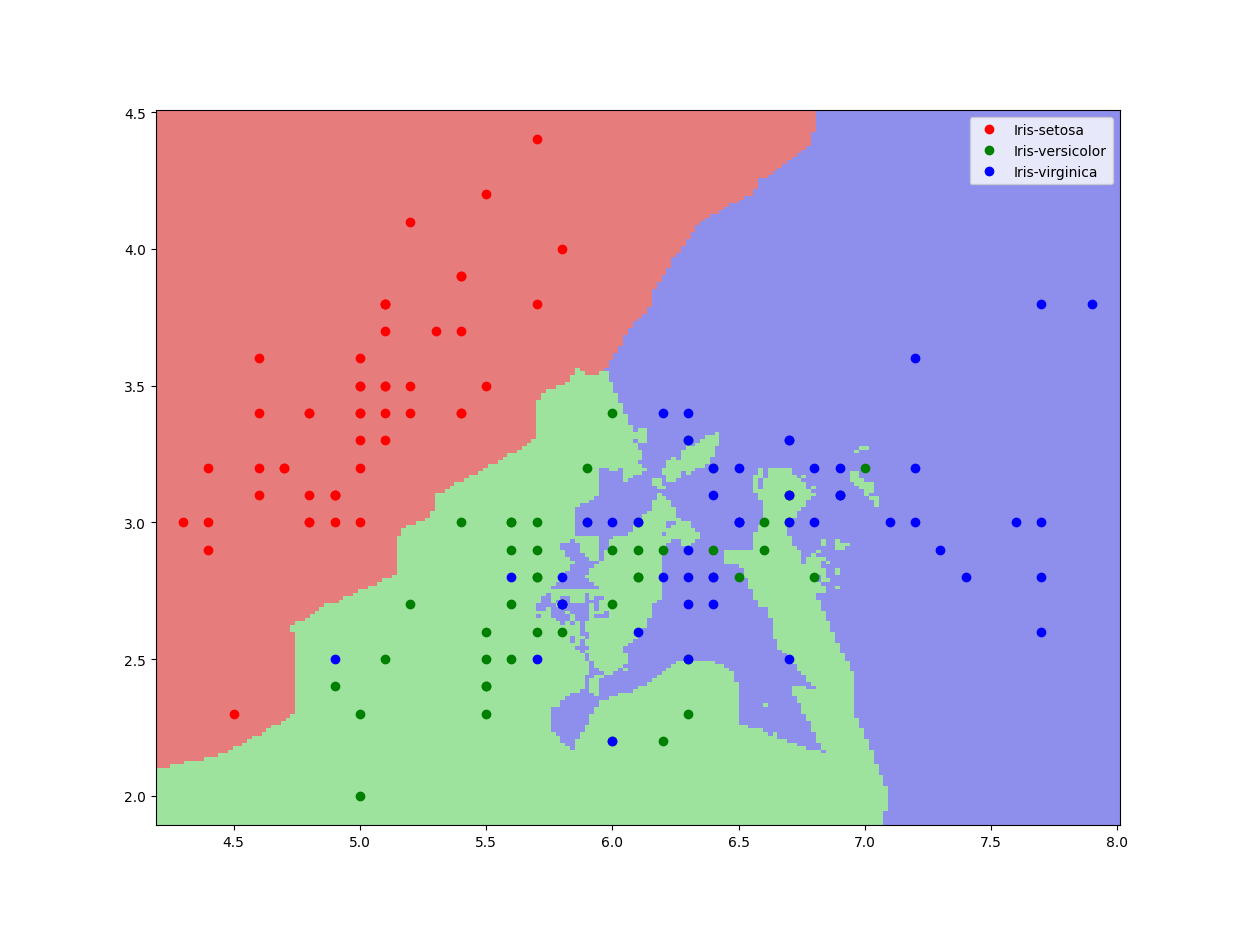
As we can see, it does a good job of separating the 3 classes, with some outliers in the dataset being contained in the wrong boundary. Below is a result of training the model using the original, unnormalized data.

Conclusion

The K-Nearest Neighbors classifier is a simple yet effective algorithm for classification tasks, particularly when the decision boundary is non-linear. By leveraging the proximity of training examples, KNN can adapt to complex patterns in the data without making strong assumptions about the underlying dataset. However, since it retains a large proportion of the training examples, the size and speed of the model can become an issue if the dataset becomes very large. In the case of the Iris dataset, the KNN classifier demonstrated high accuracy in classifying iris species based on their sepal and petal measurements.